힙(heap)
- 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료 구조
- 여러 개의 값에서 최댓값 또는 최솟값을 빠른 속도로 찾을 수 있도록 만들어진 자료 구조
- 힙 트리에서는 중복된 값을 허용합니다.
- 파이썬에서는 일반적으로 배열로 구현하는 것이 좋습니다.
- 힙(Heap)은 완전 이진 트리의 일종이기 때문에, 왼쪽에서 오른쪽으로 노드를 채워나갑니다.
- 힙의 규칙

- 힙의 노드 생성 순서는 위 그림 네모 칸 안의 숫자와 같이 생성됩니다.
- 현재 노드를 N이라고 했을 때 다음의 규칙이 성립
- 현재 노드의 번호 = N
- 왼쪽 자식 노드의 번호 = 2N
- 오른쪽 자식 노드의 번호 = 2N+1
힙 구현
1. heapq 모듈
1) heapify
- heapq.heapify(x)
- 자료구조 list를 heap의 형태로 바꿔줍니다.
import heapq
k = [9, 5, 1, 3, 7]
print(k) # [9, 5, 1, 3, 7]
heapq.heapify(k)
print(k) # [1, 3, 9, 5, 7]
2) heappush
- heapq.heappush(x, n)
- list에 heap구조의 형태( 완전 이진트리 )를 가져가면서 값을 넣어줍니다.
import heapq
h = []
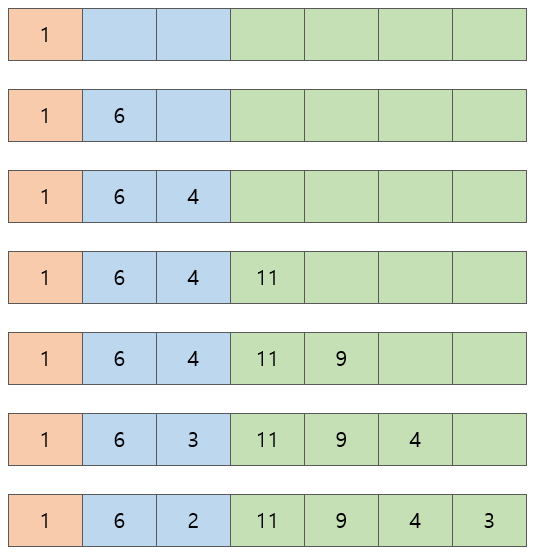
heapq.heappush(h, 1) # [1]
heapq.heappush(h, 6) # [1, 6]
heapq.heappush(h, 4) # [1, 6, 4]
heapq.heappush(h, 11) # [1, 6, 4, 11]
heapq.heappush(h, 9) # [1, 6, 4, 11, 9]
heapq.heappush(h, 3) # [1, 6, 3, 11, 9, 4]
heapq.heappush(h, 2) # [1, 6, 2, 11, 9, 4, 3]
3) heappop
- heapq.heappop(x)
- list x에서 가장 최솟값을 추출합니다.
- 연속으로 사용할 경우에는 기존의 list에서 최솟값이 계속 앞으로 이동되기 때문에 주의하여 사용해야 합니다.
import heapq
h = [1, 6, 2, 11, 9, 4, 3]
heapq.heappop(h) # [2, 6, 3, 11, 9, 4]
heapq.heappop(h) # [3, 6, 4, 11, 9]
heapq.heappop(h) # [4, 6, 9, 11]
heapq.heappop(h) # [6, 11, 9]
4) heappreplace
- heapq.heappreplace(x, item)
- list x에서 최솟값을 추출하면서 item을 추가합니다.
- heappop(x)와 heappush(x, item)를 이어서 쓴 경우와 동일한 결과이지만, 더 효율적으로 실행할 수 있습니다.
import heapq
h = [1, 6, 2, 11, 9, 4, 3]
heapq.heapreplace(h, 5) # [2, 6, 3, 11, 9, 4, 5]
heapq.heapreplace(h, 8) # [3, 6, 4, 11, 9, 8, 5]
5) heappushpop
- heapq.heappushpop(x, item)
- item을 추가하면서 list x에서 최솟값을 추출합니다.
- heappush(x,item)와 heappop(x)를 이어서 쓴 경우와 동일한 결과입니다.
- heappreplace와 동일한 결과를 보여주지만, 반대의 과정으로 진행합니다.
import heapq
h = [1, 6, 2, 11, 9, 4, 3]
heapq.heappushpop(h, 5) # [2, 6, 3, 11, 9, 4, 5]
heapq.heappushpop(h, 8) # [3, 6, 4, 11, 9, 8, 5]
5) heapmerge
- heapq.merge(x, y)
- merge()안의 요소 x,y를 최소 힙을 사용하여 하나의 정렬된 반복자(iterator)로 만들어줍니다.
- 이때, x,y는 정렬된 상태이어야 최소 힙의 형태를 정확히 나타낼 수 있습니다.
- 대량의 정렬된 데이터(x, y)를 한 번에 로드하지 않고, 필요한 만큼 조금씩 읽어와서 효율적으로 병합합니다.
import heapq
# 정렬되지 않은 값을 넣었을 때
list1 = [1, 6, 11, 3]
list2 = [2, 9, 4, 8]
h = list(heapq.merge(list1, list2)) # [1, 2, 6, 9, 4, 8, 11, 3]
# 정렬된 값을 넣었을 때
list3 = [1, 3, 6, 11]
list4 = [2, 4, 8, 9]
h2 = list(heapq.merge(list3, list4)) # [1, 2, 3, 4, 6, 8, 9, 11]- 값이 달라진 이유
- merge는 x,y의 첫번째 요소를 가져오고, 가져온 요소들을 최소 힙(min heap)에 저장합니다.
- 힙에서 가장 작은 요소를 반환 후, x,y에서 다음 요소를 가져오고 이와 같은 행동을 반복합니다.
1) x의 1, y의 2를 비교 후 '1' 반환
2) x의 6, y의 2를 비교 후 '2' 반환
3) x의 6, y의 9를 비교 후 '9' 반환 .....
- 따라서 원래의 예상 값인 [1, 2, 3, 4, 6, 8, 9, 11]과 다른 [1, 2, 6, 9, 4, 8, 11, 3]이 생성됩니다.
- 즉, merge 안의 요소들은 정렬된 상태를 가지고 있어야 합니다.
import heapq
# heapq.merge( x,y, key=None, reverse=False )
# reverse 속성 사용
# 이 때, x,y는 내림차순으로 정렬되어 있어야 합니다
list1 = [11, 6, 3, 1]
list2 = [9, 8, 4, 2]
list(heapq.merge(list1, list2, reverse=True)) # [11, 9, 8, 6, 4, 3, 2, 1]
# key 속성 사용
# 이 때, 2번째 인자로 정렬하고 싶으면 각 k, k2의 2번째 인자가 정렬되어 있어야 합니다
k = [(1, 3), (2, 5), (4, 7)]
k2 = [(8, 9), (11, 10)]
list(heapq.merge(k,k2, key=lambda x:x[1])) # [(1, 3), (2, 5), (4, 7), (8, 9), (11, 10)]
6) nlagerst
- heapq.nlargest(n, x)
- list x에서 가장 큰 요소를 n개 만큼 가져옵니다.
import heapq
h = [1, 6, 2, 11, 9, 4, 3]
heapq.nlargest(2, h) # [11, 9]
heapq.nlargest(4, h) # [11, 9, 6, 4]# key 속성 사용 가능
import heapq
h = [(1, 7), (2, 5), (4, 3)]
heapq.nlargest(2, h) # [(4, 3), (2, 5)]
heapq.nlargest(2, h, key=lambda x : x[1]) # [(1, 7), (2, 5)]
7) nsmallest
- heapq.nsmallest(n, x)
- list x에서 가장 작은 요소를 n개 만큼 가져옵니다.
import heapq
h = [1, 6, 2, 11, 9, 4, 3]
heapq.nsmallest(2, h) # [1, 2]
heapq.nsmallest(4, h) # [1, 2, 3, 4]# key 속성 사용 가능
import heapq
h = [(1, 7), (2, 5), (4, 3)]
heapq.nsmallest(2, k) # [(1, 7), (2, 5)]
heapq.nsmallest(2, k, key=lambda x : x[1]) # [(4, 3), (2, 5)]
1. 최소 힙 (Min Heap)
- 부모 노드의 값이 자식 노드의 값보다 작거나 같은 완전 이진 트리
- Root Node가 가장 작은 값을 가지고 있습니다.
import heapq
h = []
heapq.heappush(h, 1)
heapq.heappush(h, 6)
heapq.heappush(h, 4)
heapq.heappush(h, 11)
heapq.heappush(h, 9)
heapq.heappush(h, 3)
heapq.heappush(h, 2)
print(h)
2. 최대 힙 (Max Heap)
- 부모 노드의 값이 자식 노드의 값보다 크거나 같은 완전 이진 트리
- Root Node가 가장 큰 값을 가지고 있습니다.

# 방법 1
# 튜플(tuple)을 사용
h = [1, 6, 2, 11, 9, 4, 3]
h2 = []
max_h = []
for i in h:
heapq.heappush(h2, (-i, i))
for i in range(len(h2)):
max_h.append(heapq.heappop(h2)[1])
# max_h = [11, 9, 6, 4, 3, 2, 1]
# 방법 2
h = [1, 6, 2, 11, 9, 4, 3]
h2 = []
max_h = []
for i in h:
heapq.heappush(h2, -i)
for i in range(len(h2)):
max_h.append(-heapq.heappop(h2))
# max_h = [11, 9, 6, 4, 3, 2, 1]힙의 활용 예시
- 최솟값, 최댓값 n개를 구할 때
- 작업 스케줄링 ( 우선순위를 활용 )
- 이벤트 스케줄링
- 네트워크 라우팅 ( 데이터 패킷의 전송 경로를 결정하는 라우팅 알고리즘 )
- 우선순위 큐
※ 참고
[자료구조] Heap(힙) - 개념, 종류, 활용 예시, 구현
우선순위 큐를 위해 만들어진 자료구조우선순위 큐(Priority Queue)?우선순위의 개념을 큐에 도입한 자료구조데이터들이 우선순위를 가지고 있어 우선순위가 높은 데이터가 먼저 나간다!완전 이진
velog.io
[Python] heapq 모듈
Python heapq 모듈 사용법 heapq 모듈에 대한 내용에 들어가기 앞서.. heap에 대한 내용은 아래 블로그 포스팅을 참고하시면 이해하시는데 도움이 될 것 같습니다. [자료구조] 우선순위 큐와 heap 우선순
kjhoon0330.tistory.com
[자료구조] Heap (python heapq)
우선순위 큐에 대한 설명 [파이썬 알고리즘] 10장 우선순위 큐 (priority queue) with Heap 우선순위 큐 우선순위 큐의 정의 우선순위 큐의 구현 Heap Heap의 정의 Heap의 구현 Heap에서의 insert / delete (Up-Heap, D
hyoeun-log.tistory.com
'Python' 카테고리의 다른 글
| [Python] 문자열 관련 함수 -2- (0) | 2023.05.24 |
|---|
